How do you diagnose unbalance using vibration analysis?
Technically speaking, unbalance—some people say imbalance—exists when the mass center line and the geometric center line do not coincide. What does that mean and why is it important?
Let’s say we have a disk that’s perfectly balanced. I’m going to add a 2 g weight near the edge and just let the disk rotate. You are probably familiar with this idea: it’s just a single plane, and it will keep going until that weight is at the bottom. But I’m going to start the machine and let it wobble. And now we can see (in an animation in the video) that one cross is the geometric centerline and the center of the disc. The other one is the center of mass because that 2 g weight pulled it off. Therefore, we get a circular movement, and it’s that once-per-revolution movement that we’re trying to measure, and the diagnostic tools are there to prove that’s going on.
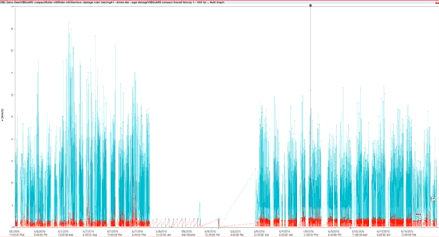
Purely from a spectrum point of view, we expect to see a great big peak at the running speed or turning speed, of the shaft. It will be visible in the vertical and horizontal axes and potentially in the axial axis as well. The time waveform will be sinusoidal if the vibration is dominated by the unbalance and if we’re looking at it in displacement or velocity (this fault condition is harder to see in acceleration).
Phase analysis, and comparing vertical to horizontal, can help us diagnose unbalance. So if we have just a single-plane unbalance—any sort of unbalance—if I compare the vertical vibration to the horizontal, because it’s trying to move in a circular motion, I expect a 90-degree phase difference between vertical and horizontal. You may think, wouldn’t that be the case with all faults? As the shaft turns, whether it is bent or there is eccentricity or misalignment or whatever, isn’t it always going to move in a circular motion? No, it is not. Even with unbalance, it doesn’t move exactly in a circular motion because of stiffness (we’ve got another video on that). As a result, we expect this 90-degree phase relationship, so the tails in the animation show 90 degrees between vertical and horizontal.
In this animation, I can see that the shaft goes up and down perfectly in phase with the other side of the shaft. There’s no rocking or anything like that. And if I compare phase from either end, it will confirm unbalance.
If I have an overhung rotor, I will still see that radial vibration—the vertical and horizontal motion. But when it’s overhung, I also get that axial rocking. Therefore, I get a vibration in the axial direction. So if I compare vertical to horizontal, I still expect to see the 90-degree relationship. There’s no need to grease between these points. I will see that there’s axial vibration, and between the two bearings, it will be in phase. But there won’t be a distinct phase relationship between these two just because of the way the rotor has to sort of flex. The ratio of vibration will be different depending on the configuration.
If I’ve got a machine—we’ll call it a longer rotor, a two-plane—with a different distribution of weight, we get what’s called dynamic unbalance. We will still see the 90-degree relationship between vertical and horizontal, but when we compare the vibration on the shaft on either side or the bearings on either side, it won’t be perfectly in phase as it would be with static unbalance (what we saw in the first case). If it happened to be pure couple, which is unlikely in reality, this would be 180 degrees out of phase. Instead, we see somewhere in between, and we call that dynamic unbalance.
In summary, if we see a high 1X peak in the vertical and horizontal directions, it indicates a high likelihood of unbalance. If it’s an overhung rotor, I should look for that in the axial direction as well. If I look at the waveform and it’s very sinusoidal in displacement and velocity, it would make me think, even more so, that it’s unbalanced (although in this case, the spectrum tells me that). I’m going to look for a phase relationship between vertical and horizontal (this is explained in much more detail separately). We’re looking for 90 degrees, but it could be anywhere from 60 to 120 degrees. But if I can measure on either side of the rotor and it’s in phase, roughly, then I would say it’s static and I can probably balance it with a single weight. If it’s opposite, if it’s much more than 120 or less than 60, I would assume dynamic unbalance, and I would probably need to do a two-plane balance.